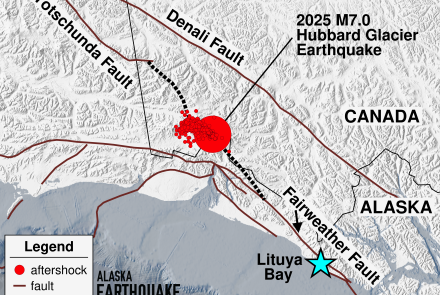
Doubling Trouble
There is an old story that tells of a philosopher who did a great service for a king. "Name your reward," cried the grateful monarch. "Anything in my kingdom is yours."
"Bring me a chessboard," said the philosopher, "and on the first square place one grain of wheat, on the second, two grains, on the third, four grains, so that each square has twice the number of grains as the square before, up to the sixty-fourth and last square of the board."
"What, so little?" asked the king. "Surely your service deserves more than this!"
"Oh king," replied the philosopher, "know that I have asked for more grain than exists in your entire kingdom, nay, than in the entire world."
In fact, the mass of grains of wheat to be placed on the final square of the chessboard would be of the same order as the mass of the entire biosphere of our planet -- jungles, forests, grasslands, animals, herbs, humans and bacteria combined.
If repeated doubling were no more than a curiosity of such tales, we could ignore the story as an odd quirk of mathematics. In fact, repeated doubling is an inescapable result of any system in which the increase over a given short time interval is a constant fraction of the amount present at the start of the time interval. As an example, a population growing at 1% per year will double every 69 years. A savings account with interest of 5% per year will double in 14 years. And an inflation rate of 10% per year brings about a doubling of prices in 7 years. Population growth, compound interest (in debts as well as savings accounts) and inflation are all examples of this kind of system.
There was recently a good deal of publicity about the earth's population reaching 5 billion people. In fact, statistics on births or deaths are not nearly good enough to know exactly when this point was reached, let alone identify the 5 billionth person, but it probably did happen (or will) in 1987. Just to see what the current world-wide population growth rate of 1.9% a year means in the long run, let's see what would happen if we assume that growth does in fact stay constant at that rate.
A growth rate of 1.9% corresponds to a doubling time of 36 1/2 years. If we started out with 2 people, we would have 5 billion people after about 31 1/2 doublings of the population -- just about half of the doublings of the philosopher's chessboard. If the population had been growing at its current rate throughout human history, Adam and Eve would have lived in A.D. 848! Obviously, our current rate of population growth is much greater than the average over human history.
What about the future? With our present population of 5 billion, we have about 7 acres of land area (including ice sheets, deserts, and increasing amounts of pavement) for each human being on the globe. In only about 100 years at current growth rates, that would be down to 1 acre a person. By some time in the 26th century, we would be down to a square yard of land area per person, and a bit more than a century after that, to a square foot. Even the most determined advocate of population growth could hardly consider a global population density well in excess of the crowding in a present-day commercial airliner to be desirable or feasible, or argue that the trampled earth could grow food for so many.
In nature, growth of a population is a temporary response to a sharp lowering of numbers or a sudden increase of resources available. Here in Alaska, snowshoe hares have periodic spells of rapid population growth. Eventually the population becomes large enough to put so much pressure on food plants that they become toxic, to attract an increase of predators, or to support an epidemic, and the result is a catastrophic decline. Our own current population growth resulted from our ability to control predators (except other humans) and disease (though AIDS may yet prove an exception). Will we be able to check our population growth by our own decision, or will war, pestilence, and famine do it for us?