Escape Velocities

In high school, my cherished turtle-back '49 Ford wasn't the newest thing on the road, but it was reasonably reliable. It was about this time, at the beginning of the space age in the early '50s, that people began to talk about "escape" velocities, and other esoteric quantities that I didn't quite understand.

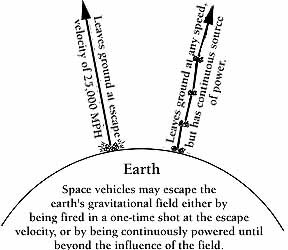
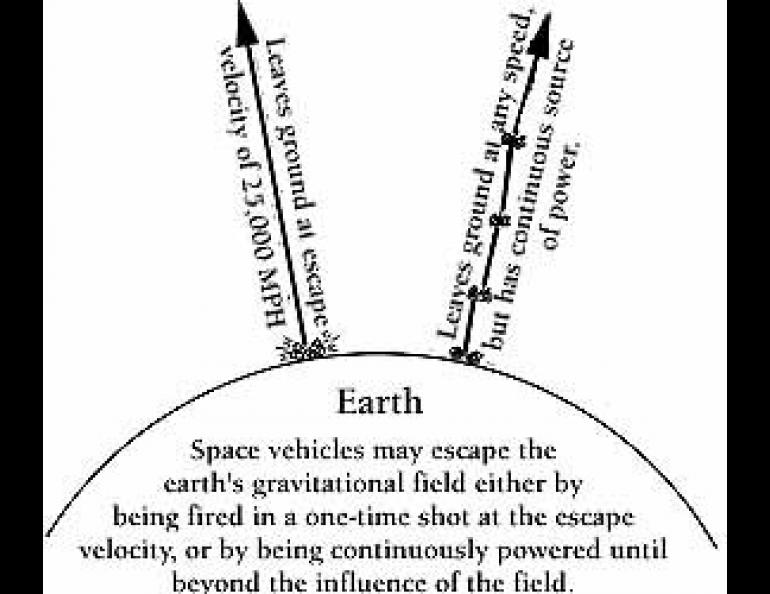
When we were told that the escape velocity from the earth was on the order of 25,000 miles per hour, that didn't make much sense to me. I would lie awake in bed at night and wonder why, given enough gas and a suitable dirt road, I couldn't just poke the nose of my old Ford up, plod off at a sedate 30 mph or so, and eventually travel far enough from the earth to escape its gravitational field.

It was years later that I found out that in theory, if not in practice, it would have been possible. If a continuing source of power were available, anything, including rubber bands would do for escape, providing they had sufficient lifting power to get the mass off the ground in the first place, and could last the interminable amount of time that it would take to travel the distance required.

The term escape velocity as used in celestial mechanics is usually applied to a surface launch velocity, disregarding aerodynamic friction. Such an example would be the velocity of a projectile fired from a cannon in an airless environment.

It is not necessary for a space vehicle to achieve escape velocity in order to obtain orbit (as a matter of fact, if it did, it could never return without some means of slowing down). A circular orbit is achieved at 0.71 times the escape velocity, which is why we often hear of the value of about 17,500 mph (earth's escape velocity X 0.7) for orbiting satellites and space ships.

At velocities higher than that needed to obtain a circular orbit, the path becomes elliptical until escape velocity is approached, at which time the orbit becomes parabolic. At velocities greater than the escape velocity, it becomes hyperbolic, and the object escapes into space.

The more massive the celestial body, the greater the escape velocity. For instance, the escape velocity on the Moon is only about 3000 mph; for the planet Mercury, about 7900 mph; for Mars, about 11,000 mph; and for giant Jupiter, a whopping 133,000 mph.

This is why the great planets such as Saturn and Jupiter have such dense atmospheres, and the smaller planets such as Mercury and the Moon have none. Escape velocities on the giants are much too high for even high-speed gas molecules to escape, while the smaller planets do not have enough gravity to hold onto them.

Fortunately for us, this is why the earth continues to have an atmosphere. The mean velocity of the atmospheric gas particles is much lower than the earth's escape velocity. By comparison, Mars' gravity is such that the planet has already lost most of its atmosphere, and is barely hanging on to the little it has left.