Koch's Snowflake, Mandelbrot's Coastline
Journalists love numbers almost as much as scientists do, and probably for the same reason: if you can put an exact number on it, it must be real.
That was never more clear than during the oil spill in Prince William Sound. Readers, listeners, and viewers were given numbers for everything from how many gallons are in a barrel of oil to the dollar value of the annual pink salmon catch. They were told how many sea otters lived near Naked Island and how many square miles of sea water lay under the oily scum. Yet in all the news of threatened coastline, rare indeed were statistics on the length of that coastline.
At first, that doesn't seem logical. A coastline is obviously real, so it must be measurable in real numbers. Well, yes and no. Contemporary mathematics, with roots in the early part of this century, raises some doubts.
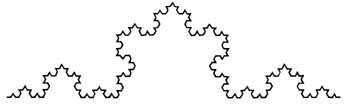
In 1904, the Swedish mathematician Helge von Koch described an interesting curiosity. He proposed a mental exercise that could be partially carried out in visible form by anyone with pencil, paper, and patience.
Draw an equilateral triangle, with each side equal to a unit--say, one foot. Then, to the middle of each of the triangle's sides, attach another triangle of the same shape but with its sides equal to one-third the length of the sides of the parent triangle. If the original's sides were a foot long, then each side of the new form would be four inches long. Instead of three points, there are now six; instead of three sides, there are now 12. This new form would look exactly like the traditional Star of David.
Repeat the process, adding new triangles a third the size of the preceding ones to the middle of each of the 12 sides. What appears looks rather like the end of a medieval mace. With a few more repetitions, the shape looks like an idealized snowflake.
Theoretically, the process can go on and on. No matter how detailed the drawing, the outline is continuous. The new triangles on each side are always small enough to avoid bumping into one another. The length of the outline can be calculated by simple arithmetic: 3 x 4/3 x 4/3 x 4/3 -- except that the series of calculations can be taken to infinity. Yet the area of the figure enclosed remains limited, and very little larger than the area of the original triangle. In fact, if you drew a circle around the original triangle, the Koch snowflake would never extend beyond that circle, no matter how many times you added new triangles.
Koch had shown that a finite area can be enclosed by an infinite line. Serious mathematicians of the time found this repulsive. It ran counter to intuitive geometry. It was unnatural. It was ignored--almost.
In the 1960s, Koch's snowflake resurfaced in the hands of another mathematician given to upsetting his colleagues. Benoit Mandelbrot looked at the snowflake's edge and saw "a rough but vigorous model of a coastline," as he later said. From that, he posed a question in the title of a paper: How long is the coast of Britain?
Mandelbrot's answer was as valid for the oiled edge of Prince William Sound as for Britain. In a sense, any coastline can be taken as infinitely long, just as the edge of Koch's snowflake can be infinitely long. In another sense, its length depends entirely on the length of your ruler.
More specifically, it depends on how much of nature's extraordinary detail your ruler can follow. Tie one end of a ball of twine to a runner's ankle, and have your athlete gallop along the edge of a bay. Measure the unrolled twine at the end of the run, and you'll get a certain length for the shoreline. If you could tie the twine to a snail's tail and have the little beast crawl the shore from end to end, you'd get a much greater length. Pebbles ignored by the runner would have to be crawled around by the snail, and the increased detail would increase the measured length of the shoreline greatly. A determined amoeba would have to ooze an even greater distance to trace the shore.
The real limit may be at the subatomic level--perhaps.
So, a truly honest reporter would have to say that the threatened coastline was nearly infinite in length, and even longer when the tide's out. Of course, no newspaper readers would believe that--unless they knew about Koch's snowflake and Mandelbrot's coastline.