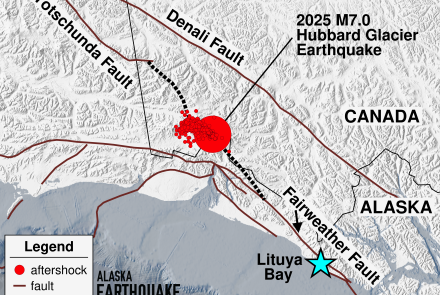
Nature's Golden Ratio, Part II
Seldom has an article appearing in this space generated the volume of reader response as did last month's column on the Golden Ratio. The interest shown seems to justify a sequel.
To recapitulate briefly, the Golden Ratio consists of the two numbers 1.618034 and 0.618034, each of which is the reciprocal of the other. Rectangles with sides proportioned 0.618034 to 1 (or 1 to 1.618034) are often the shape taken by such commonplace items as picture frames and playing cards.
Thus, the shape seems to be subliminally pleasing to the human eye, as witnessed by the many ways in which it is used in art and in construction. It is also found in nature, reflected in essentially every spiral form from a snail shell to the arms of a galaxy.
The earlier column told only half the story of the Golden Ratio, however. Historically, credit for recognition of the peculiar mathematical properties of this ratio must go to a 13th century Italian known as Fibonacci. The "Fi" part of his name meant "son of." The Bonacci part meant "simpleton."
Although history does not record the mental acuity of Fibonacci's father, it does relate that the boy took an early interest in the number of rabbits that could be raised in a year if one began with a single pair. Fibonacci reasoned that, if the rabbits reached maturity two months after birth and produced an additional pair every month thereafter, the total population of rabbit pairs would increase monthly according to the series 1, 2, 3, 5, 8, 13, 21, 34...
This deceptively simple-looking series is obtained merely by sequentially adding numbers which are the sum of the preceding two. It is permissible at this point to ask what all this has to do with the Golden Ratio, and therein lies the beauty.
If you take the quotient of any two numbers in the Fibonacci series, you will find that the further you go up the line, the closer the value converges on the "perfect" ratio. For example, 2 divided by 3 equals 0.6666... (and 3 divided by 2 equals 1.5), but 21 divided by 34 equals 0.6176... (and 34 divided by 21 equals 1.6190...). Eventually,the quotients become precisely the numbers in the Golden Ratio and remain that way.
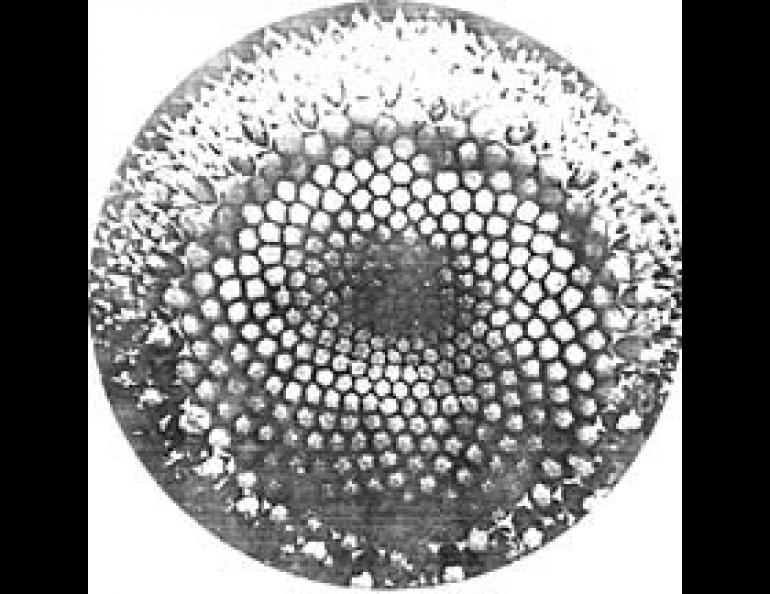
Nature finds a myriad of ways to put these numbers to work. Most are so commonplace that we never take notice of them. The individual florets in the head of a daisy grow in two spirals extending out from the center. One spiral has 21 arms; the other has 34. These are two adjacent Fibonacci numbers. A pine cone has two spirals of 5 and 8 arms, and a pineapple has spirals of 5, 8 and 13--all Fibonacci numbers (I must confess that, although I was finally able to identify the spirals on a pineapple in the supermarket, I got hopelessly lost on a white spruce cone).
But these are only a sampling. Most of nature's horns, claws and teeth (including your own) exhibit a Fibonacci spiral. Even though the curvature is slight, any dentist knows that he must pull a tooth in the right direction.
Returning to mankind's application of the Golden Ratio: While I was stationed in Europe many years ago, I learned to appreciate the fact that converting between miles and kilometers was simplified because they were related to each other by the reciprocal factors 1.6 and 0.6. Do you suppose...?