Predicting The Tanana Breakup

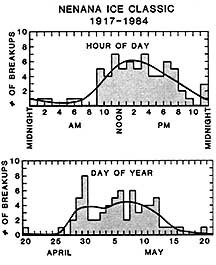
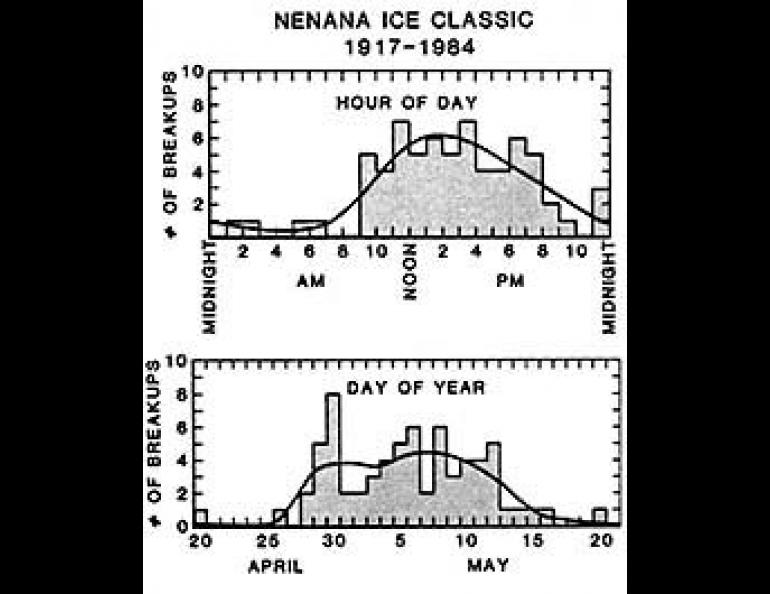
In May 1976, this column carried an article by John Miller and Neil Davis that presented probabilities for the Tanana River ice going out on particular dates and hours. Their calculations were based on records that had been kept for the Nenana Ice Classic since its inception in 1917.

Miller and Davis downplayed the seriousness of the diagram which they produced, suggesting that it could perhaps be put to best use by hanging it on the wall and aiming at its center with darts. Nevertheless, they noted that the data from past breakups indicated that the most probable minute for the ice to go out lay during the hour between 12:00 noon and 1:00 P.M. on May 6. They also noted that this had not yet occurred during the history of the Classic.

The following year, on May 6, 1977, two of the most flabbergasted people in the state of Alaska must have been John Miller and Neil Davis when the ice went out at 12:46 P.M. 

That initial success has not been repeated, but with the addition of the intervening nine years to the existing "data set," it might be time to take another shot at it.

Miller and Davis did not explain precisely how they arrived at their probability figures, but I suspect that it was akin to the method used here, which gives very similar results.

First, because there are no nice, regular curves to deal with in trying to match the past observations with a mathematical function, it is necessary to "smooth" the data. That is, if one just plots a bar-graph of dates and times, there are bars sticking out all over the place with gaps in between, and it's pretty hard to deal statistically with something that has "corners" like that. To compensate for this, the data were smoothed by moving a "window" across the set, taking into consideration not only the particular point in question (day or hour), but also the two to either side of it.

Based on the past record, the probability that the ice will go out during a particular hour of a particular day can be assumed to be the percentage of times that it has gone out during that hour multiplied by the percentage of times that it has gone out on that day. For example, taking the hour between 6 P.M. and 7 P.M. on May 5: the ice has gone out five times on May 5 in 68 years (7.35 percent of the time), and between 6 and 7 P.M. on six occasions (8.82 percent of the time). Thus, the probability that it should go out on May 5 between 6 and 7 in the evening would be 0.0735 times 0.0882, or 0.00648. Picking only a single minute during this hour takes one-sixtieth of that chance, resulting in the probability of a hit being slightly less than 1 in 10,000. Using the smoothed data for that particular "window" further lowers the probability by about one-quarter, but this still leaves it as one of the better bets.

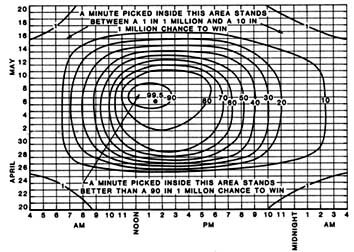
If the smoothed data are used to repeat this process for each of the 744 one-hour time frames between April 20 and May 20 (the earliest and latest dates on which the ice has gone out), the resulting matrix can be contoured to show periods of relatively high and low breakup probability.

The data indicate that based on past performance, the premier slot would be a minute between 1 P.M. and 2 P.M. on May 6. The calculations for minutes within that hour indicate a 99.5 in one million chance of success. This compares well with the value of 96 chances per million given by Miller and Davis for the hour between 12 P.M. and 1 P.M. on May 6 that they calculated nine years ago.

Lest anyone be tempted to take all of this too seriously, it pays to remember that more winners in the Nenana Ice Classic split the pot into smaller and smaller portions each year. Further, it is debatable just how significant statistics like these really are. For instance, it can be questioned whether it is meaningful to overlay a diurnal (daily) trend on a monthly one. It might be argued that this is like equating apples with oranges.

But that wouldn't matter anyway to those unsung heroes who, year after year, place their bets on January 1st or July 31st. That's like bidding $1 on The Price Is Right. After all, it's the game that counts.