Surfaces
Centuries ago, architects discovered that a practical way to design structures that combined minimum weight with maximum strength was to experiment with soap bubbles. They would bend a wire frame to the outline of a vaulted alcove, for example, and dip the framework into a bucket of suds. The shape assumed by the soap film on the wire outline defined the most economical form for the walls in the real structure.
Although workers at the time probably did not know it, they were experimenting with forms called "minimal surfaces." A minimal surface has the property that any section of it has the least possible area, given the boundaries to which it must adhere. Even today, scientists find that playing with soap bubbles is a quick way to gain insight into certain problems that would take laborious hours of mathematical computations to simulate. Nature is a superior mathematician.
The most common minimal surface with which we come into contact every day is the sphere--a free-floating soap bubble, for instance. The sphere encloses the greatest possible volume with the least possible surface area. The tension in a soap film insures that there are no loose edges flapping around.
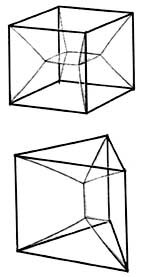
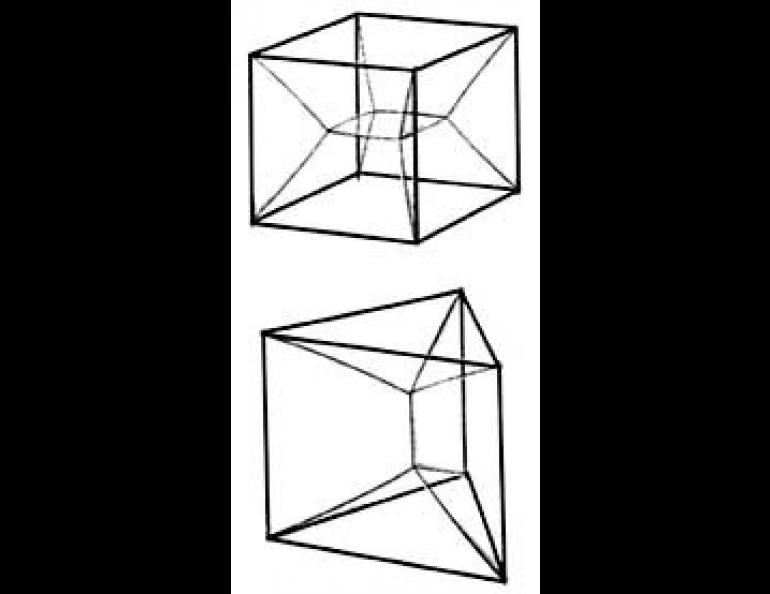
Sometimes the minimal surfaces that are formed can be unexpected. Most people would assume that dipping the outline of a cube into a soap solution would result in a bubble shaped like a child's building block. It doesn't. The minimal surface connecting all the edges of a cube has walls that slope inward, meeting at angles of 120 degrees around a small square at the center. Similar shapes result from dipping triangular wire prisms and other more complicated forms. The inviolable rule is that whenever three films meet, they do so at the same angle of 120 degrees.
While it might at first appear that the minimal surfaces of a sphere and a cube should have many of the same properties, they actually belong to entirely different "subsets." A sphere has no edges, no boundaries; you could begin tracing a path around a sphere and continue forever without interruption.
Until recently, there have been only three minimal forms known to science which have this property. One is the plane, extended outward forever to infinity. Another is the sphere. The third looks like a saddle and is called a hyperbolic paraboloid (great subject for a dinner conversation). In fact, some scientists believe that all of space may be curved in one of these forms. If we live in a "closed" universe, space would be curved like the sphere. An "open" universe would be curved like the saddle, Most of us can come to grips only with the planar universe with straight-lines that go to infinity the way they're supposed to--but we're almost certainly wrong.
For 200 years these three forms were the only known examples of the subset of minimal surfaces that have no edges and don't intersect themselves. Mathematicians have long suspected that there are others, but the computations involved in defining them are horrific, and it's difficult to attach soap bubbles to infinity.
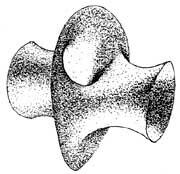
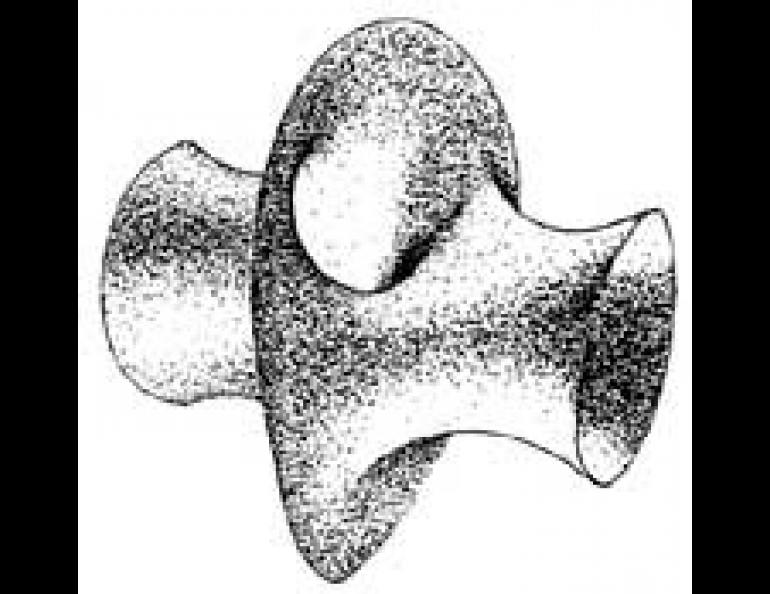
The next-best thing to soap bubbles, reasoned David Hoffman of the University of Massachusetts and William Meeks of Rice University, would be to have a computer simulate one. So they did. The object appearing on the screen was unlike anything seen or imagined before, but knowing what it looked like gave Hoffman and Meeks the information they needed to perform the mathematics which defined its shape.
The new candidate, which looks something like a plumbing T-joint wearing a ballerina skirt, may be the first of a whole new line of abstract minimal forms. Before we leap to question what they are good for, it would be well to remember that simpler minimal surfaces found many practical applications in the past.