The Cannon Ball Express
Much of what follows appeared in this column over four years ago. Judging from reader response, it was one of the most popular columns to appear in this space. Some recent callers have requested that it appear again. Here it is:
A matter which has been debated since the days of early Greece is the question of what would happen to an object dropped into a hole that extended through the center of the earth.
Galileo was the first to assess the outcome correctly. If one were to drop, say, a cannon ball into such a hole it would fall with increasing speed, but decreasing acceleration, until it reached the exact center of the earth where its speed would be about 18,000 miles per hour and the acceleration would be zero. Subsequently, its speed would decrease with increasing deceleration until it reached the opposite side of the earth, at which point it would fall back again. If it were not for air friction, it would continue yo-yo-ing back and forth in this manner forever.
In actuality, such an event, even if it were possible, could happen only if the hole were drilled from pole to pole. At any other orientation, the Coriolis effect of the earth's rotation would soon have the ball bouncing off the walls of the tunnel.
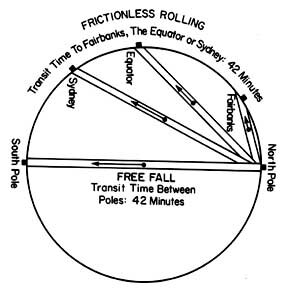
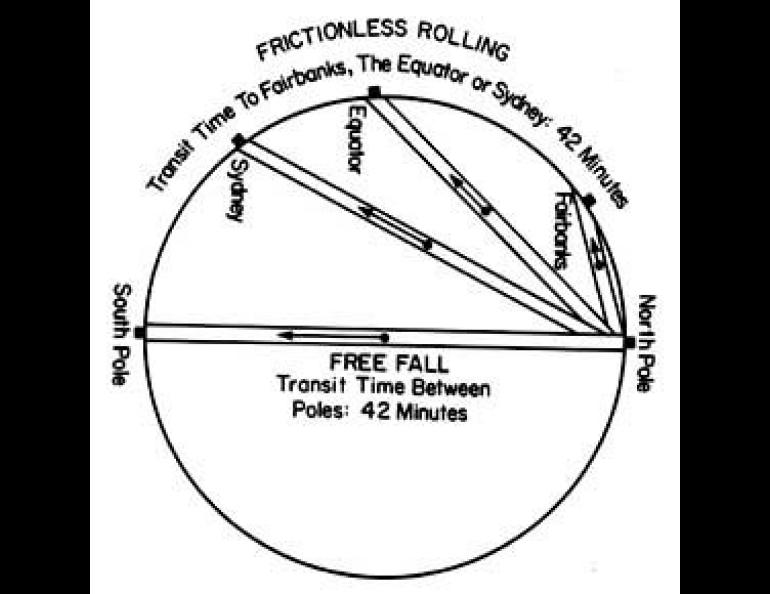
A fascinating variation to this theme is one that has appeared in several works of fiction. If a perfectly straight tunnel were to be drilled between any two points on the earth's surface, it would be theoretically possible to travel from one end of the tunnel to the other without using any power at all (assuming zero friction).
Due to curvature of the earth, the midpoint of the tunnel would be closer to the earth's center than either end, and for the first half of the trip, the train or car would be traveling downhill. Halfway through the tunnel, it would have achieved precisely the amount of momentum required to carry it the remaining uphill half of the trip.
What is difficult to believe about this unlikely scenario is that the time required for the trip would be the same regardless of the length of the tunnel! Theoretically, it could be a few miles, a few thousand miles, or through the center of the earth. The time of transit in all cases would be just over 42 minutes.
(James A. Raymond of Fairbanks wrote a sequel to this article in which he proved mathematically that, while the "straight-line" hypothesis is valid, a really "faster" path to two points on the earth's surface is shaped something like a clothesline draped between two suspension points. In the case of the pole-to-pole drop, the path becomes a straight line.)