A Faster Ride on the Cannonball Express
Back in April, this column covered the fate of a cannonball dropped into a tunnel extending right through the center of the earth to the other side. That cannonball (or any object) would yo-yo back and forth, from surface to surface forever--if only there were a way to make the tunnel frictionless.
The best part of the whimsy, though, is that a perfectly straight frictionless tunnel connecting any two points on the earth's surface would permit effortless travel, with the cannonball (or a Cannonball Express with passengers) accelerating downhill for the first half of the trip and coasting uphill to the surface for the last half. Better yet, the travel time through such a tunnel connecting any two points on the globe would be exactly the same: Fairbanks to Anchorage in 42 minutes, Anchorage to Antarctica in 42 minutes.
Many readers were inspired to send in comments about that article, and one even offered an improvement on tunnel design. James A. Raymond of Fairbanks correctly observed, "Some tunnels are faster than others". Using the calculus of variations, he went on to demonstrate that the fastest path is one shaped something like the line formed by a rope hanging between two poles.
Such a curve, called a catenary, is only an easy-to-visualize approximation of Raymond's ideal tunnel shape, which he calls a "circular cycloid."
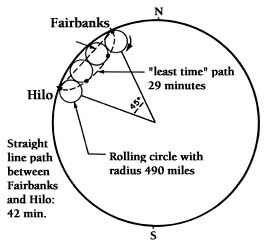
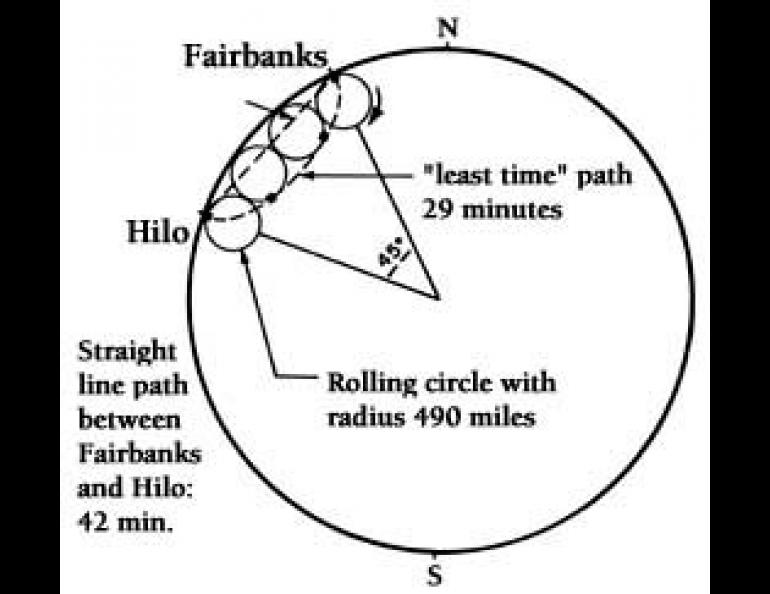
A cycloid is the path traced out by a spot on the rim of a wheel as it rolls along. Assume that the spot is in contact with the ground when the wheel begins to roll. At the end of one-half revolution, it will be at the top of the wheel, and after a complete revolution it will be in contact with the ground again, but down the track a distance equal to the circumference of the wheel. A line connecting all points occupied by the spot during the short trip is a cycloid.
The only difference between this curve and Raymond's circular cycloid is that, in the latter case, the wheel is rolling around the inside of a larger circle instead of on a flat surface.
If the surface of the earth is taken as the larger circle, Raymond proves that the path of least travel time for a freely coasting tunnel traveler would be a circular cycloid connecting the two end points of the tunnel.
For example, to plot such a path between Hilo, Hawaii, and Fairbanks would require an imaginary wheel with a radius of about 490 miles. The trip along the circular cycloid would take the coaster about 29 minutes, as compared with the 42 minutes that it would take in the conventional straight tunnel.